Over the past decade, the importance of incorporating uncertainty analysis into climate modeling has become generally recognized. The question is whether our current tools are up to the task. I've been looking at this question and my paper on it, "Uncertainty analysis comes to integrated assessment models for climate change...and conversely," has just been published in Climatic Change (available as an open access publication). My conclusion is that we need a serious investment in a new generation of of uncertainty quantification techniques to address the difficult issues that the climate problem raises.
Developments in uncertainty quantification have largely been driven by large methodology investments in the nuclear sector which produced three generations of uncertainty quantification.
The first generation building off the Reactor Safety Study (1975) introduced structured expert judgment in uncertainty propagation and distinguished variability and uncertainty. The second generation (1991) emerged in modeling the physical processes inside the reactor containment building after breach of the reactor vessel. Operational definitions and expert judgment for uncertainty quantification were elaborated. The third generation focused on the consequences of release of radioactivity and transport through the biosphere. Expert performance assessment, dependence elicitation and probabilistic inversion are among the hallmarks. You can find background in this RFF discussion paper and in a special issue of Radiation Protection and Dosimetry.
Applications of third generation in current Integrated Assessment Models of climate change reveal daunting issues of model uncertainty. As an illustration from the article, integrated assessment models such as DICE let climate damages hit (only) economic output; they enter the capital growth equation at the one third power. As a result, growth follows a differential equation solved by Jakob Bernoulli in 1695, whose properties are well known.
With constant population and constant productivity of labor, capital converges at an exponential rate to an equilibrium value independent of the starting capital. The two capital growth trajectories shown below start our world with ten times the current capital level (dotted) and one dollar (solid), other parameters chosen from DICE 2009. In 60 years the trajectories are indistinguishable. With one dollar the world could not afford one shovel and the consequences of such a shock are likely to be remembered longer than 60 years.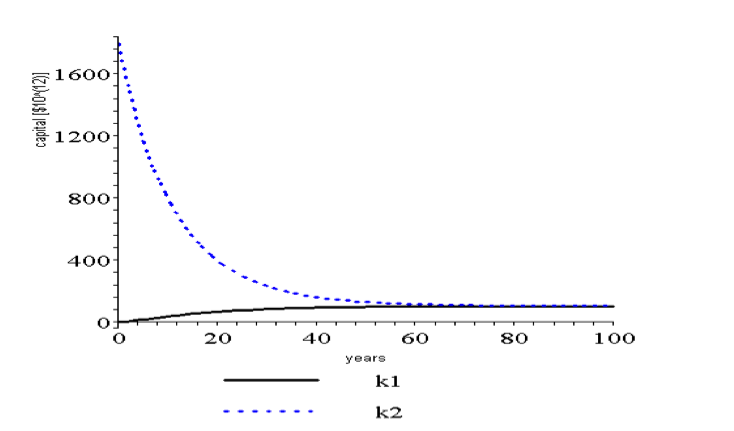
An uncertainty analysis must circumscribe the domain of applicability of the Bernoulli dynamics. For example there are alternative approaches such as using a predator prey relation between production and pollution lead to a Lotka Volterra dynamics in which Gross World Product first rises, and then collapses then oscillates around an equilibrium level.
(For more detail see here)