Value of Science 203: The Value of Scientific Information When Future Outcomes Are Uncertain

In previous explainers, we introduced the VALUABLES Impact Assessment Framework as a tool to demonstrate the value of new Earth science information from satellites. Completing the framework requires scientists to identify the actions a decisionmaker takes and the socioeconomic outcomes of those actions in two states of the world: one with and one without the new information. Our main example was an ex post, or retrospective, evaluation of the benefits of using satellite data to inform closures and advisories for recreation at Utah Lake during a harmful algal bloom. Another example was an ex ante, or future-looking, assessment to examine how satellite data that are available but not being used could help marine shipping operators comply with future regulations to conserve Pacific blue whales at lower cost. In both cases, the impact assessment team was able to identify actions and outcomes in the states of the world with and without the information—even in the ex ante assessment of the information that was yet to be used. But what happens when an impact assessment team is trying to estimate the value of information yet to be used, in scenarios marked by uncertainty about future outcomes?

For example, consider the case of a more accurate hurricane prediction system. Let’s say the federal government already has directed resources to this system, and as a result, decisionmakers had access to improved forecasts when a hurricane made landfall. Using the VALUABLES Impact Assessment Framework, you could conduct an ex post analysis of its value by quantifying the number of lives saved due to more timely evacuations, or property damage averted due to improved targeting of sandbagging activities based on the improved forecasts. This calculation would require you to compare the number of deaths from the hurricane, or cost of property damage, to the deaths or damage that likely would have occurred had decisions been made without the improved forecast.

Now imagine that the hurricane prediction system does not yet exist, and the question is whether funding its creation is cost-effective. How do we know the value of improved hurricane forecasts before the hurricanes happen? This context requires an ex ante analysis that estimates the value of improved hurricane forecasts for hurricane-related decisions that will take place in the future. The value of the improved forecasts will depend on the attributes of future hurricanes, yet the frequency, severity, and location of future hurricanes are unknown to you when you are doing the impact assessment.

These kinds of impact assessments are very difficult to conduct and have rarely been performed in the context of valuing scientific information—but they are possible, and at minimum, we can learn how to conceptualize these values. In this explainer, we introduce some useful concepts and methods—developed by mathematicians and economists over centuries, and used in everyday contexts, from setting insurance premiums to investing in stocks and innovation—for how to think about the value of improved information when it has yet to be used and the future is uncertain.

Imagine you are making a financial decision; a textbook example would be whether to purchase a lottery ticket. A concept that comes in handy is expected value, which establishes the value of different options under uncertainty. More specifically, expected value can be defined as the sum of the value of each potential outcome multiplied by the respective probabilities that the outcomes occur. In the lottery example, two outcomes are possible: losing and winning. Thus, if you have a one-in-a-million chance of winning a $1-million jackpot, the expected value of the ticket looks like the following:

Expected value of buying a lottery ticket = (Probability of winning x Value of winning) + (Probability of losing x Value of losing)

= (0.000001 x $1,000,000) + (0.999999 x $0)

= $1

So, paying more than $1 for a lottery ticket would be a bad investment, because the cost of buying the ticket exceeds its expected value.

Or let’s say a school wants to host an outdoor fundraiser. They plan to invest $1,000 and make $2,000 in sales. But if it rains, the school will have to cancel the fundraiser and forfeit the sales. The weather forecast calls for a 20% chance of rain. Is it a good investment? In this case, the expected value of the fundraiser looks like the following:

Expected value of outdoor fundraiser = (Probability of no rain x Profit) + (Probability of rain x Expenditures)

= (0.8 x $1,000) + (0.2 x –$1,000)

= $800 – $200

= $600

In both examples, the decisionmaker did not know with certainty which outcome would be realized—whether they would win the lottery, or whether it would rain on the day of the fundraiser. However, the concept of expected value allows them to place a single value on the uncertain outcomes.

More specifically, to conceptualize the ex ante (expected) value of improved information in the presence of uncertainty, one first has to specify the set of contingencies or scenarios, i.e., the possible set of future events, outcomes, or states of the world.

To return to the hurricane example from the introduction of this explainer, in a simplified set of scenarios for a potential hurricane, the contingencies could be the following:

(1) no hurricane
(2) weak hurricane
(3) moderate hurricane
(4) severe hurricane

The next step is to assign a societal value to each one of these scenarios. For example, for the four hurricane contingencies, the value of the outcomes presumably is highest for scenario (1) and lowest for scenario (4). Then, assign probabilities of occurrence to each scenario. The probabilities must each be non-negative and sum to exactly one across the scenarios. For example, you might assign a high probability to scenario (1) and a low probability to (4), consistent with the notion that severe hurricanes are rare.

The expected value is the weighted average of values over all the scenarios, where the weights are the respective probabilities that the scenarios occur.

The expected value of information is the increase in the expected value due to a reduction in the uncertainty. In the last two examples, the expected value of information would be the answer to the question, What is the value of the weather forecast? To arrive at this value requires a different calculation.

In the hurricane example, suppose that in addition to being exposed to a potential hurricane, the decisionmaker has at their disposal some actions that may reduce the negative societal impacts of a hurricane, such as evacuation, preparedness, or emergency response measures. Taking these actions will be valuable if a hurricane happens (especially a severe one) because the actions will reduce deaths and property damage. However, these actions also are costly—evacuations and other measures are very expensive and time consuming. So, the decisionmaker is faced with deciding between actions that are costly but potentially highly beneficial without knowing with certainty which hurricane outcome will happen.

How do we think about the value of improved information in this decision context? First, note that the probabilities that a decisionmaker assigns to each of the four contingencies are based on information they have about how likely it is for each type of hurricane to occur in a given place at a given point in time. Now, suppose that new information—an improved hurricane forecast—provides more accurate probabilities that each hurricane outcome will happen. In general terms, this information clearly has value if a decisionmaker is more likely to implement evacuations and other costly measures when the hurricane turns out to be severe, and less likely to implement these measures when no hurricane happens. In other words, when the decisionmaker has access to the new forecast, they still may not know whether the hurricane will be weak or severe, or if a hurricane will happen at all, but they are more likely to take the correct action because the probabilities they assign to each hurricane outcome are more accurate. This improved likelihood of taking the correct action is the expected value of the information; the availability of improved information makes it more likely that the decisionmaker will take a better action. Much like the value of information when outcomes are certain, which requires you to compare the value of outcomes with and without the improved information, the expected value of information involves comparing the expected value of outcomes when actions are chosen with the improved information and the expected value of outcomes when actions are chosen without the information.

The hurricane example helps us think about the value of scientific information when future outcomes are uncertain by relying on the concept of expected value. However, this example also shows the difficulty of quantifying the expected value. To estimate the expected value of an improved hurricane forecast, the impact assessment team must know not only the difference in probabilities of the hurricane outcomes between the existing and improved forecasts, but also the monetized cost of deaths and property damage from each possible hurricane outcome, and the reduction in those negative impacts that results from the various actions that the decisionmaker can take. Such an analysis quickly becomes complicated in decision contexts that have many outcomes and many possible actions that a decisionmaker can take. The section below illustrates how the expected value of information can be calculated, using a relatively simple example with two possible actions and two potential outcomes.

A classic example of the expected value of information comes from work published by James P. Quirk in 1976 and Molly Macauley in 2005. Imagine a farmer can harvest her entire crop today at a cost of $10,000, or she can harvest it over two days (today and tomorrow) for $2,500 per day, representing a savings of $5,000. The harvest is worth $50,000. What is the value to the farmer of a weather forecast that could say with certainty whether there will be enough heavy rain tomorrow to preclude harvesting?

As Macauley explains:

Table 1 indicates the “payoff” to the farmer in the event of heavy rain. In expected-value terms, these payoffs are $40,000 with decision A and (p) ($22,500) + (1 – p) ($45,000) with decision B. If p = 5 / 22.5, then the decisions give the same payoff if the farmer is “risk neutral.” If the farmer were risk averse, she would want a lower value of p before waiting to harvest.

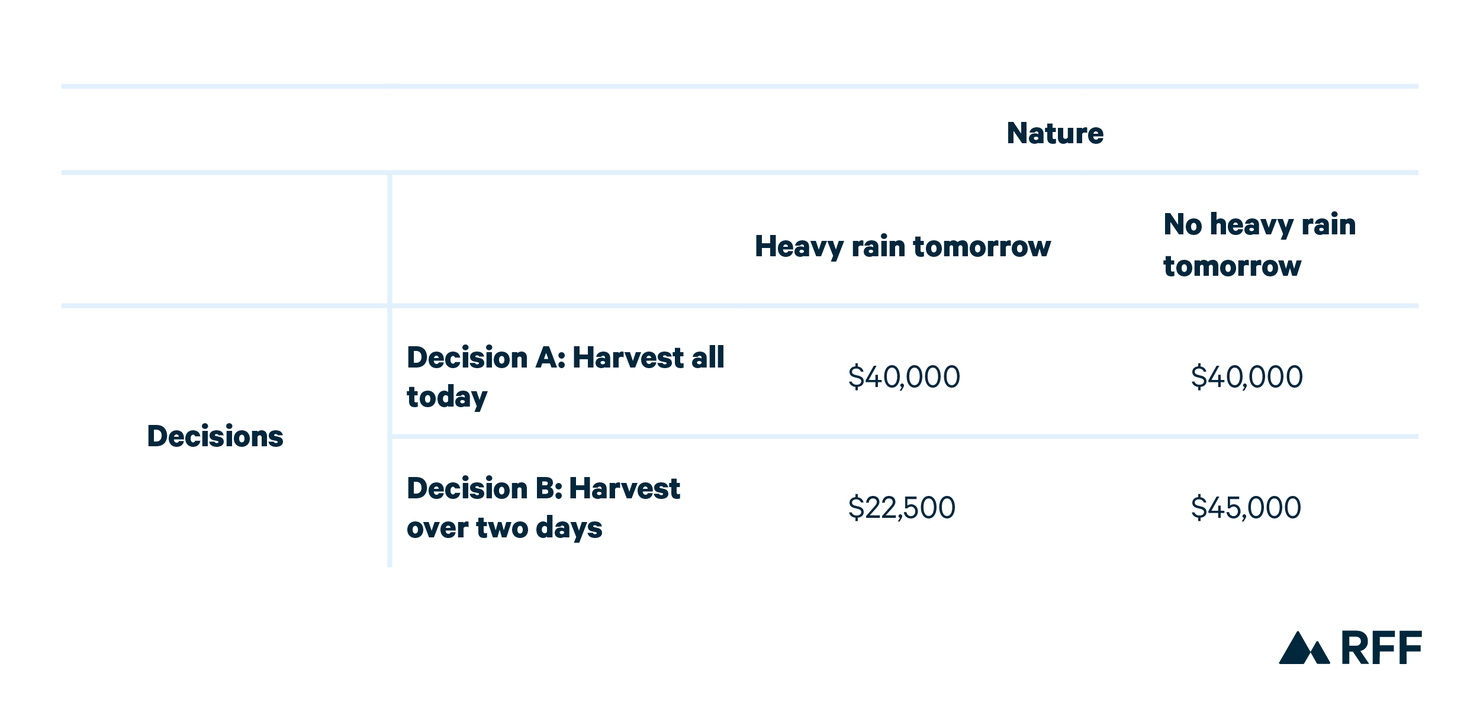
If forecasting the weather is possible, then p is the probability that the farmer receives information that a heavy rain will happen tomorrow with certainty (and (1 – p) is no rain, with certainty). Since p is a subjective probability, it can vary among different farmers. The expected payoff with information is then

(p) ($40,000) + (1 – p) ($45,000)

If $x is the highest amount of money the farmer would pay for information, then $x is equal to the difference between the expected payoff with information, and the expected payoff without information. The value of information varies with p as in Figure 1.

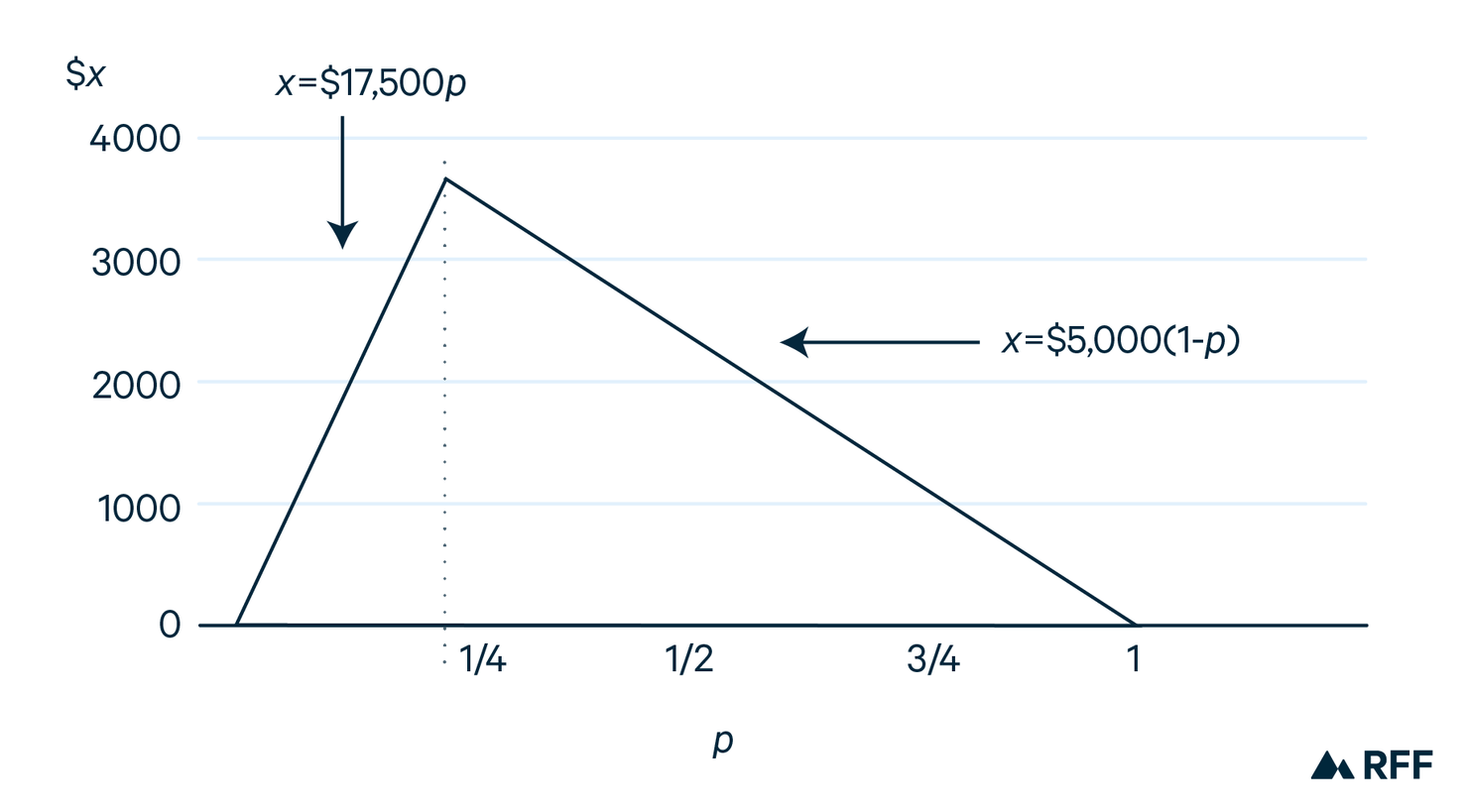
The value is maximized at p = 5 / 22.5 (where $x = $3,888); as above, this is the p at which the farmer flips a coin. Information can thus make the biggest difference here. The value of information is zero at p = 0 and p = 1, since at these extremes, the farmer is already certain in her own mind whether it is going to rain, and information is extraneous (even if the farmer is wrong).

Applications of the model can show the effects of changing the amount or quality of information as well as subsequent revisions that the individual may make to the probability.

Another complicating factor when assessing the expected value of scientific information in the context of uncertain future outcomes is that the estimated value of information is subjective. The fact that the expected value of information is subjective has several implications. First, it means that the expected value of any given set of improved information may vary across decisionmakers. Second, it means that the expected value of information for a particular decisionmaker depends on their beliefs about the probabilities of various future outcomes in the absence of the improved information.

These two implications of the subjectivity of the expected value of information, in turn, lead to a key insight that we introduced in the Value of Science 105 explainer: the benefits of improved information are likely to be largest when the information greatly reduces uncertainty and enables actionable decisions with big impacts. In contrast, if a decisionmaker who has yet to receive the improved information is highly certain about the occurrence of a future outcome (i.e., they assign a probability close to 0 or 1 to a particular contingency), then the expected value of information will be small. Note that this is true even if the decisionmaker is wrong about the probabilities they assign to future outcomes—the expected value of information is low if you are highly confident about what will happen in the future, even if you are wrong! The example above also illustrates this point.

In the end, Earth science data provide a host of information that decisionmakers can use to assess the probabilities of various states of the world. When the information sharpens the accuracy of these probabilities (i.e., the likelihood of rain or a hurricane) and allows us to make better decisions, that information is a resource that has socioeconomic value.